2. Equilíbrio de Hardy-Weinberg
O Teorema de Hardy e Weinberg é o fundamento
da genética de populações, descrito em 1908 independentemente pelos dois pesquisadores, e demonstra uma simples relação matemática entre frequências alélicas e genotípicas em uma população, que leva a uma importante previsão dentro da genética de populações:
“As
frequências alélicas e genotípicas tendem a permanecer em equilíbrio nas populações em
panmixia e na ausência de fatores evolutivos”.
Equilíbrio significa que para cada frequência alélica vai corresponder uma distribuição de frequências genotípicas!
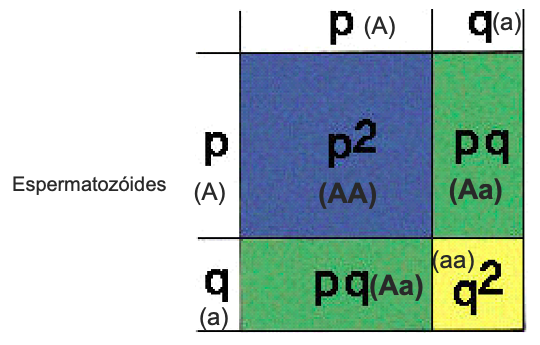
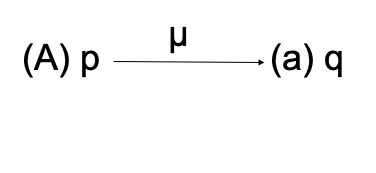
Freq alelo A = p então, Freq genótipo AA = pxp = p2
Freq alelo a = q Freq genótipo Aa = 2pq
Freq genótipo aa = qxq = q2
Para que o equilíbrio se mantenha e as frequências se mantenham constantes, há dois pressupostos:
a. panmixia = todos os indivíduos de uma população tem a mesma chance de se cruzar com qualquer outro indivíduo da população (ausência de cruzamentos preferenciais).
b. ausência de fatores evolutivos:
•População infinita (o que garante a ausência de
deriva genética)
•População isolada (sem fluxo gênico, não recebe novos alelos nem perde alelos)
•Todos os genótipos têm o mesmo
valor adaptativo (ausência de
seleção
natural)
•Os
genes são constantes (não ocorrem
mutações ou as
taxas de mutação são desprezíveis)
O teorema de Hardy-Weinberg só é válido para organismos diplóides,
de reprodução sexuada e gerações discretas (não sobrepostas, indivíduos de gerações diferentes não se cruzam).
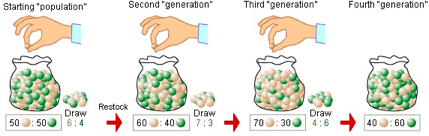
O equilíbrio é alcançado em apenas uma geração! Ou seja, qualquer população cujas frequências não estejam em equilíbrio, em apenas uma geração em panmixia sem ação de fatores evolutivos as frequências atingem o equilíbrio.
Mas as condições estabelecidas para a obtenção do equilíbrio de H-W não são completamente
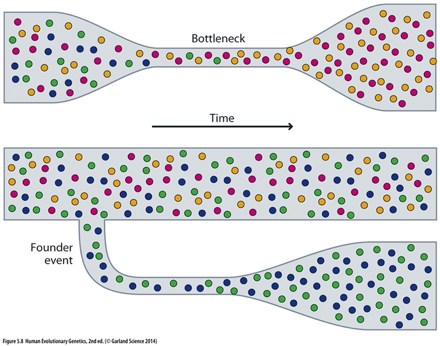
satisfeitas por nenhuma população real! Nenhuma população real é infinita, então todas as populações sofrem algum grau de deriva genética. E é isso torna possível explicar o processo evolutivo dos seres vivos (ação de fatores evolutivos). Apesar disso, os genótipos se distribuem de acordo com
o equilíbrio de
Hardy-Weinberg para muitos caracteres monogênicos que não suscitam casamentos preferenciais. As taxas de mutação em geral são muito baixas, a deriva genética tem em geral impacto pequeno, a seleção natural só atua fortemente em algumas regiões do genoma e os cruzamentos preferenciais, quando ocorrem, são baseados em um pequeno número de características.
•Para um gene com dois alelos, “A”
e “a”:
Frequência do alelo “A”
= p
Frequência do alelo “a”
= q
•p + q = 1
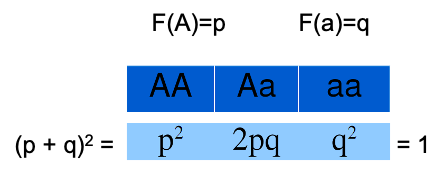
•As frequências genotípicas na população se distribuem de acordo com o binômio:
É possível demonstrar matematicamente como essas frequências se mantém ao longo das gerações:
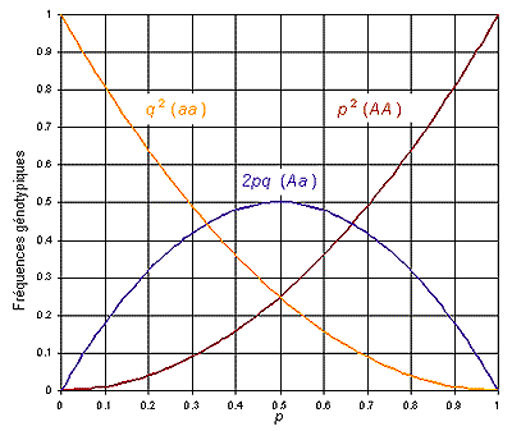
O equilíbrio de H-W também pode ser representado de uma forma gráfica, onde podemos observar que a frequência máxima de heterozigotos em uma população em equilíbrio é de 50%, o que ocorre quando os dois alelos apresentarem frequência de 50%.
Cálculo (contagem) de frequências alélicas quando há codominância (os heterozigotos são diferenciados dos homozigotos, ou temos a informação molecular):
Fatores
que alteram as frequências
genotípicas
sem alterar
as frequências
alélicas:
•fuga
da panmixia: cruzamento preferencial
- homogamia (cruzamento preferencial entre indivíduos portadores do mesmo alelo) aumenta a
taxa de homozigose
(inclusive de genes letais).
- heterogamia (cruzamento preferencial entre indivíduos com alelos diferentes) favorece a heterozigose.
- Endogamia (ou endocruzamentos, casamentos consanguíneos): casamento
entre indivíduos geneticamente aparentados em frequência maior do
que a esperada ao acaso. A consanguinidade (indivíduos com ancestralidade comum) leva ao aumento na probabilidade de homozigose por origem comum do
gene.
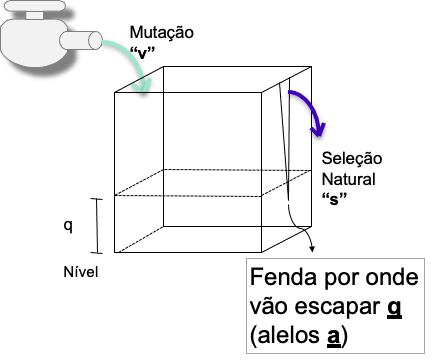
Fatores evolutivos: que alteram as frequências alélicas nas populações:
•Determinísticos:
com intensidade, direção e variância determináveis
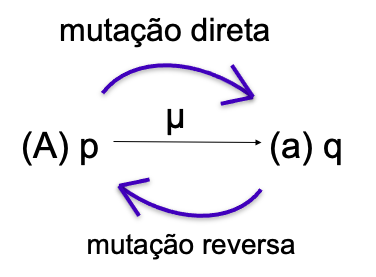
- Mutação
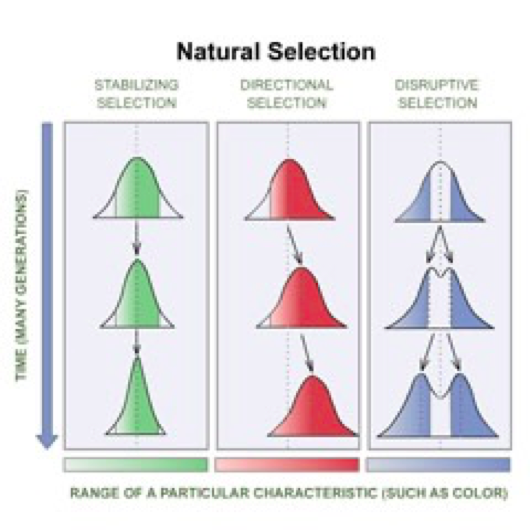
- Seleção
natural
- Migração (fluxo gênico)
•Estocásticos: sem direção determinável
- Deriva genética